|
Источники питания со сглаживающими дросселями были очень популярны в период расцвета ламповых усилителей по одной простейшей
причине, а именно из-за отсутствия конденсаторов с очень большой емкостью. Поэтому для сглаживания пульсаций после выпрямителя
должны были использоваться дроссели (рис. 6.14).
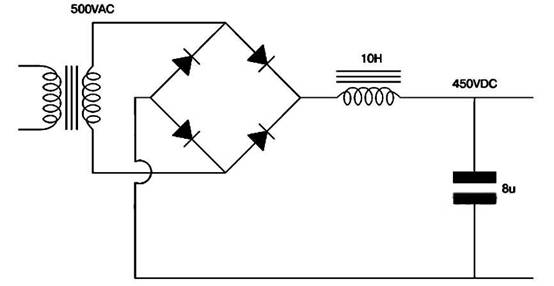
Рис. 6.14 Источник питания со сглаживающим дросселем
Если бы представилась возможность изготовить источник питания со сглаживающим дросселем, в котором величина индуктивности
дросселя имела бы бесконечно большое значение, то ток в силовом трансформаторе был бы полностью идентичен постоянному току,
протекающему в нагрузке.
На практике источники питания никогда не достигают этого идеала, поэтому ток вторичной обмотки трансформатора представляет
собой комбинацию постоянного тока нагрузки и меньшего по величине и приближающегося по форме к синусоидальному, тока дросселя.
Тем ни менее, источник питания со сглаживающим дросселем имеет огромное преимущество, заключающееся в том, что он обеспечивает
почти неизменный по величине ток, протекающий в цепи от силового трансформатора, а не последовательность коротких импульсов
с высокими значениями размаха тока, как при работе выпрямителя на накопительный конденсатор. Для того, чтобы понять, почему
это происходит, необходимо очень внимательно рассмотреть форму напряжения на выходе выпрямителя (рис. 6.15).
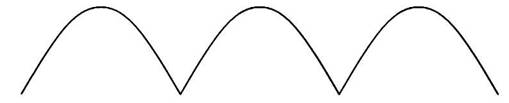
Рис. 6.15 Форма напряжения после двухполупериодного выпрямления
После двухполупериодного выпрямления, выходное напряжение имеет вид, привеенный на данном рисунке, однако, так как от
претерпевает нелинейный процесс выпрямления, набор частот, образующих этот сигнал, отличается от набора частот (фактически
одного колебания с частотой 50 Гц), поступающих на вход выпрямителя. Анализ Фурье показывает, что результат выпрямления чисто
синусоидального сигнала можно представить в виде суммы высших гармоник:
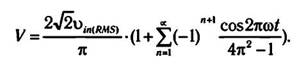
Необходимо учесть, что член υm(RMS) в формуле
является напряжением сигнала до его выпрямления.
Приведенное выше уравнение является математической формой представления периодического сигнала несинусоидальной формы
в виде теоретически бесконечного ряда синусоидальных колебаний (гармоник) на частотах, кратных частоте повторения сигнала.
На практике, говоря о гармониках непериодического сигнала, всегда ограничиваются их конечным числом, поскольку интенсивность
гармоник убывает с ростом их номера. Учитывают только те гармоники, которые образуют примерно 95% общей энергии сигнала.
Результат вычисления коэффициентов Фурье (то есть амплитуд гармоник) для нашего частного случая двухполупериодного сигнала
дает следующее:
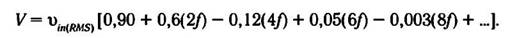
Последнее выражение показывает, что сигнал синусоидальной формы после двухполупериодного выпрямления можно представить
набором (или суперпозицией), состоящим из постоянной составляющей (постоянного напряжения), равного
0,90υm(RMS), и последовательности
уменьшающихся по амплитуде четных гармоник, кратных частоте (f) исходного синусоидального сигнала.
Таким образом, для фильтрации переменных составляющих выпрямленного тока, целесообразно использовать дроссель имеющий
очень высокое реактивное сопротивление для на частотах этих переменных составляющих, поэтому только постоянная составляющая
выпрямленного тока будет протекать в нагрузке выпрямителя со сглаживающим дроссельным фильтром. Выходное напряжение источника
питания со сглаживающим дросселем, таким образом, будет составлять 0,9υm(RMS), что значительно отличается
от значения √2υm(RMS), характерного для источника питания с накопительным конденсатором.
Минимальный ток нагрузки для источника питания со сглаживающим дросселем
К сожалению, для правильной работы источника питания со сглаживающим дросселем требуется наличие некоторого минимального
тока, протекающего в нагрузке. Если величина потребляемого нагрузкой тока меньше этого минимально допустимого значения, выпрямитель
возвращается к состоянию, когда происходит заряд конденсатора (теперь уже речь идет о сглаживающем конденсаторе, включенном
после дросселя) импульсами напряжения и выходное напряжение возрастает до максимального значения, равного √2υm(RMS).
Минимальное значение потребляемого тока определяется следующим выражением:
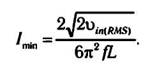
Так как на практике индуктивность дросселя частично зависит от величины протекающего по нему тока (см. кривую намагниченности
или В-Н зависимость), то следует несколько увеличить получаемое по расчетам значение. Для этого можно воспользоваться упрощенной
формулой, учитывающей такое увеличение (которая будет справедлива для сетей питания переменного тока с частотами 50 и 60
Гц):
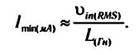
Источник питания со сглаживающим дросселем всегда работает на дополнительный сглаживающий конденсатор, в силу чего требование
к минимальному значению тока нагрузки приобретает особое значение, так как невыполнение этого условия может вызвать увеличение
напряжения на конденсаторе до значения, составляющего примерно 157% от его номинального значения, и которое может привести
к выходу конденсатора из строя. Традиционным путем решения данной проблемы является использование переключаемого дросселя, индуктивность
которого резко возрастает при малых токах, и хотя такой способ практически перестал применяться после 1960-х годов, в настоящее
время он вновь получил признание.
После увеличения тока сверх минимального значения, пульсации выходного напряжения будут постоянными по величине при изменении
тока нагрузки, а переменные составляющие выпрямленного синусоидального сигнала будут ослаблены в соответствии с выражением:
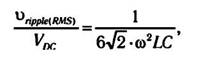
в котором ω = 2πf.
Если принять, что только амплитуда второй гармоники выпрямленного тока вносит существенный вклад в образование пульсаций,
то указанное выражение может быть представлено в следующем виде:

в которых индуктивность L выражена в генри, а емкость С в микрофарадах, а величина υm(RMS)
является напряжением на вторичной обмотке силового трансформатора.
|