|
Конденсаторы обладают способностью накапливать и сохранять электрический заряд. Заряд сохраняется на двух изолированных
друг от друга пластинках конденсатоpa,
между которыми приложено внешнее напряжение. Если напряжение между обкладками конденсатора отсутствует, то заряд
также отсутствует и принято считать, что конденсатор разряжен.
Все конденсаторы, применяемые в электротехнике, состоят из двух основных частей: пары токопроводящих пластин, или обкладок,
и изолирующего материала, называемого диэлектриком, который разделяет обкладки. В самом простом виде конденсатор состоит
из двух плоскопараллельных пластин, разделенных вакуумом.
Плоский конденсатор
Вполне очевиден тот факт, что емкость плоского конденсатора прямо пропорциональна площади А его пластин и обратно пропорциональна
расстоянию d между ними. Этого следует ожидать, так как если раздвигать пластины на бесконечно большое расстояние,
то уменьшающиеся заряды пластин не смогут взаимодействовать друг с другом, а каждая пластина по отдельности уже не будет
являться конденсатором. Если заряд накапливается на пластинах, то можно положить, что внесение любого материала k между
пластинами повлияет на емкость конденсатора, путем ослабления взаимодействия между заряженными пластинами. Вышеприведенные
аргументы можно изложить несколько формальным способом, используя следующее соотношение:
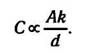
Для того, чтобы рассчитать реальное значение емкости конденсатора, необходимо ввести некоторую постоянную, характеризующую
степень ослабления взаимодействия между пластинами за счет введения диэлектрика. Из физики известно, что под действием электростатического
поля, возникающего между двумя заряженными обкладками, происходит поляризация диэлектрика, в итоге вызывающая ослабление
напряженности этого самого поля. Для учета этого явления, вместо эмпирического коэффициента k, в формулу необходимо
ввести специальные физические величины, называемые диэлектрическими постоянными: чтобы получить уравнение, приведенное ниже:
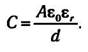
В данном выражении присутствуют две диэлектрические проницаемости: постоянная ε0 известен, как абсолютная
диэлектрическая проницаемость вакуума и для системы единиц СИ равен: ε0 = 8,854 * 10-12 Ф/м. Константа
εr., характеризует относительную диэлектрическую проницаемость материала, помещенного в качестве
диэлектрика между пластинами конденсатора, связана со значением абсолютной диэлектрической проницаемости, причем всегда
значение εr > 1.
Несложный расчет, проведенный с использованием данного уравнения, показывает, что в условиях вакуума (хотя с известным
приближением можно считать, что результат, полученный для условий воздушного зазора, будет почти идентичен результату,
полученному для условий вакуума) плоский конденсатор, имеющий площадь пластин 1 м2, и которые разделены расстоянием
10 см, будет иметь емкость 88,5 пФ. Если посмотреть на реальные схемы лампового усилителя, то это не такая уж и большая емкость,
а подобные размеры конденсатора, просто недопустимо большие. Разумеется конструкции реальных конденсаторов таковы, что их
размеры намного меньше, чем в рассмотренном примере.
Уменьшение зазора между пластинами и увеличение количества пластин
Самым простым способом увеличить емкость конденсатора без увеличения его геометрических размеров, является уменьшение
зазора между пластинами, поэтому в промышленно выпускаемых конденсаторах величина расстояния между ними составляет 5 мкм
или еще меньше.
Вторым способом является увеличение количества пластин, например, изготовление конденсатора в виде блоков из отдельных
пластин, в каждом из которых все пластины одного блока соединятся вместе (рис. 5.2). Такой прием практически удваивает емкость
по сравнению с интуитивно ожидаемым в первый момент значением, так как в этом случае используются обе поверхности каждой
из пластин (за исключением, естественно, только двух крайних пластин). Такая конструкция часто используется для слюдяных
посеребренных конденсаторов и также для объединенных в батареи пленочно-фольговых конденсаторов.
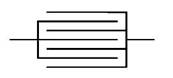
Рис. 5.2 Поперечный разрез стандартного конденсатора с параллельными пластинами
Вырезание квадратиков из диэлектрика и соответствующих металлических пластинок при изготовлении рассмотренной выше конструкции,
а затем сборка их в одну батарею является дорогостоящим предприятием, поэтому большая часть конденсаторов изготавливается
иначе. Берутся две длинные полоски фольги, являющиеся пластинами или обкладками конденсатора, между ними помещается полоска
диэлектрика, затем все это сворачивается в форме цилиндра, и в конце к каждой из обкладок присоединяются электрические выводы.
Свойства диэлектрика. Эквивалентная схема конденсатора
Изготовить конденсатор с воздушным диэлектриком, в котором воздушный зазор был равномерным и составлял бы между пластинами
точно 5 мкм по всей поверхности, практически невозможно, следовательно, между пластинами чаще всего необходимо класть разделительную
диэлектрическую прокладку. Так как используемый диэлектрик будет иметь значение относительной диэлектрической проницаемости
εr > 1, то это приведет к дополнительной возможности еще больше уменьшить геометрические размеры
конденсатора при сохранении той же самой величины его емкости. (Либо, при тех же размерах получить увеличение емкости.)
К сожалению, такой способ увеличения емкости конденсатора произойдет за счет изменения его других параметров, влияние
которых следует рассмотреть подробнее. Любой диэлектрик характеризуется тремя основными параметрами: относительной диэлектрической
проницаемостью, электрической прочностью и диэлектрическими потерями.
Относительная диэлектрическая проницаемость, εr, которая уже упоминалась выше, и является
коэффициентом, на который увеличивается (относительно случая, когда диэлектриком является вакуум) емкость конденсатора после
помещения между пластинами нового диэлектрика.
Электрическая прочность характеризует максимальную напряженность электрического поля, измеряемую в вольтах на метр, которая
может быть приложена к диэлектрику до того, как в нем произойдет пробой и он утратит свои изолирующие свойства. Этот фактор
как раз и определяет предельное значение рабочего напряжения конденсатора.
Диэлектрические потери характеризуют степень неидеальности диэлектрика и отличия его свойств от идеального при значениях
напряжения между обкладками конденсатора, не достигающих пробоя. Непосредственный способ характеризовать потери — это измерить
токи утечки, которые протекает в диэлектрике при приложении максимального значения рабочего напряжения к конденсатору (и
которые обычно выражаются в микроамперах). Этот метод обычно используется для электролитических алюминиевых и танталовых
конденсаторов. Пленочные конденсаторы, как правило, характеризуются значительно меньшими потерями, поэтому для таких конденсаторов
могут быть использованы величина сопротивления изоляции, или сопротивление току утечки. Так как диэлектрические потери могут
различаться по своей величине для случая применения конденсаторов в цепях постоянного и переменного токов, то поэтому гораздо
удобнее пользоваться такой характеристикой, как тангенс угла диэлектрических потерь, tgδ, который характеризует величину
активных потерь в диэлектрике на различных частотах. Следует отметить, что при измерении tgδ не делается различий
между параллельным сопротивлением утечки диэлектрика и любым последовательным сопротивлением, таким как сопротивление подводящих
проводов или сопротивление обкладок.
Омические сопротивления подводящих проводов и обкладок объединяются вместе и получили общее название эффективное последовательное
сопротивление (ESR). Для некоторых компонентов схем, таких как электролитические конденсаторы большой емкости,
применяемых в источниках питания или катодных полосовых фильтрах, данный параметр является очень важным,
так как он может составлять значительную часть полного импеданса конденсатора. В источниках питания в накопительных конденсаторах
протекают значительные токи, которые вызывают сильный внутренний саморазогрев структуры. По этой причине также используется
параметр, очень тесно связанный с последовательным эффективным сопротивлением, получивший название максимальная постоянная
составляющая пульсирующего тока.
Гибкие выводы обладают собственной последовательно подключаемой в схеме индуктивностью, а если не предприняты особые
меры, то пластины конденсатора также обладают собственной индуктивностью. Простая эквивалентная схема замещения реального
конденсатора выглядит следующим образом: параллельно емкости включается сопротивление потерь диэлектрика, а затем, последовательно
этой цепи — эффективное последовательное сопротивление выводов и обкладок, а также паразитная индуктивность выводов (рис. 5.3).
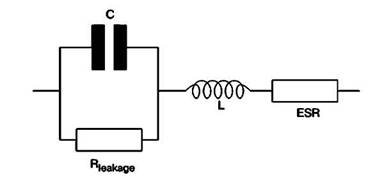
Рис. 5.3 Эквивалентная схема замещения реального конденсатора
При рассмотрении схемы сразу становится ясным, что речь идет о классическом резонансном контуре, более того, для электролитических
конденсаторов нередко частота собственного резонанса приводится в технической документации производителей. Более подробно
эта проблема будет обсуждаться позже.
|