|
Общие сведения о цифровом представлении сигналов и аналого-цифровом преобразовании
Аналоговый сигнал является непрерывно изменяющимся во времени процессом, причем величина его напряжения или тока может
плавно изменяться, принимая любые промежуточные значения в интервале от минимального до максимального. В отличие от аналогового,
цифровой сигнал несет информацию о величине (напряжении, токе) исходного сообщения лишь в фиксированные моменты времени,
а сами его значения также могут принимать только строго фиксированные дискретные значения, которые обычно представляются
в виде двоичных чисел. В качестве некоторой наглядной модели, можно обратиться к процессу измерения какой-либо зависимости.
Построение графика по нескольким точкам измерений — грубая модель аналогово-цифрового преобразования, поскольку отдельные
измерения являются фиксированными значениями. Представление аналоговых сигналов в цифровом виде (аналого-цифровое преобразование),
когда фиксированные значения исходного сигнала, взятые через определенные промежутки времени, представляются в виде двоичных
чисел очень удобно, поскольку позволяет применить к такому сигналу математическую обработку силами современной вычислительной
техники, оперирующей как раз двоичными числами.
Аналогово-цифровое преобразование (АЦП) является сложным процессом, состоящим из двух частей. Первая процедура — фиксация
процесса через определенные промежутки времени, называемая дискретизацией. Вторая процедура — приведение значения
зафиксированного параметра к одному из разрешенных дискретных уровней, называемая квантованием. На практике существуют
различные алгоритмы этих процедур, проводимых в той или иной последовательности. После преобразования, дискретные значения
заменяются определенным двоичным числом (в зависимости от конкретного значения дискретного уровня). Этот процесс называется
кодированием.
Процесс аналого-цифрового преобразования также часто называют импульсно-кодовой модуляцией (ИКМ или PCM — Pulse Code
Modulation).
Дискретизация. Теорема Котельникова - Найквиста
Процесс фиксации параметров исходного аналогового сигнала (подвергаемого АЦП) через определенные равные интервалы времени
называется дискретизацией. На
практике очень важно знать, какова требуется частота повторения выборки (фиксации параметров). Эта частота называется
частотой дискретизации. Например, если делать 96000 выборок в секунду, то частота дискретизации равняется 96 тыс.
Выборок/с или 96 кГц. Для того, чтобы непрерывный аналоговый сигнал заменить последовательностью его отдельных значений (отсчетов),
взятых (зафиксированных) через определенные равные промежутки времени, без потери полезной информации, необходимо выполнить
требования теоремы Котельникова — Найквиста. Эта теорема гласит, что для безошибочного восстановления аналогового сигнала
из его дискретных отсчетов, частота дискретизации должна быть как минимум вдвое больше верхней (наибольшей) частоты исходного
аналогового сигнала. Таким образом, на любой из частот исходного сигнала, выборка отсчета должна производиться не менее,
чем дважды за период. Работа всех устройств, использующих цифровое представление аналоговых сигналов (например, проигрывателей
компакт-дисков) базируется на этой фундаментальной теореме.
Если условия теоремы Котельникова — Найквиста не будут выполнены, аналоговый сигнал не сможет быть точно восстановлен
из цифрового. В итоге, аудиосигнал, поступающий в громкоговоритель, окажется обогащенным новыми спектральными составляющими,
являющимися продуктом специфических нелинейных искажений.
Нарушение критерия Найквиста порождает побочные низкочастотные составляющие, которых не было в первоначальном сигнале.
Чтобы предотвратить появление этих дополнительных спектральных составляющих, перед аналогово-цифровым преобразователем нужно
устанавливать фильтр нижних частот, задерживающий все составляющие исходного сигнала с частотами вдвое ниже частоты дискретизации
(обычно с небольшим запасом) и более высокими. Например, компьютерная звуковая карта, работающая на частоте дискретизации
44,1 кГц должна быть укомплектована фильтром нижних частот, обладающим частотой среза ≈ 20 кГц. Таким образом, если
использовать компьютерную звуковую карту для измерения нелинейных искажений, нужно подавлять все частоты аудиосигнала выше
20 кГц. Если же требуется точно воспроизвести сигналы, содержащие спектральные составляющие на более высоких частотах, требуется
более высокая частота дискретизации. В тоже время, работаю с цифровыми осциллографами, применение подобных фильтров нежелательно,
поскольку их частота дискретизации в процессе измерения меняется в широком диапазоне. В тоже время, всегда можно установить
а таком осциллографе заведомо высокую частоту дискретизации, что снимает проблему.
Масштабирование, квантование, кодирование
При построении графика на разграфленной бумаге важно правильно выбрать масштаб, который удобен для построения. Например,
если миллиметровая бумага имеет десять крупных квадратов, каждый из которых состоит из десяти маленьких квадратов, а измеряемый
ток находится в диапазоне от 0 до 8 мА, то нужно установить масштаб одного большого квадрата = 1 мА. Это может показаться
очевидным, но что будет, если мы выберем масштаб одного большого квадрата = 0,1 мА или 10 мА?
В первом случае, наши данные выйдут за пределы миллиметровой бумаги, а во втором случае график будет трудно разглядеть.
Назначение масштабирования — привести в соответствие диапазон параметра диапазону системы измерения.
Подобным образом, когда преобразуют аналоговый сигнал в цифровой, то сначала определяют масштаб фиксируемого параметра
(тока, напряжения), а затем осуществляют процедуру квантования. Кстати — именно по этой причине, в большинстве цифровых
вольтметров указывается их базовая погрешность в диапазоне 0—5 В. Их система измерения фактически измеряет только
в диапазоне от 0 до 5 В, а переключатель диапазонов лишь переключает аттенюаторы или усилители, чтобы привести масштаб внешнего
напряжения или тока к этому основному диапазону. В практических задачах это означает, что масштабирование не может быть точным,
следовательно оно увеличивает ошибки во всех диапазонах.
Как уже говорилось выше, квантованием называют процесс приведения уровней дискретных отсчетов к фиксированным значениям.
При этом, произвольное значение отсчета сравнивается с набором фиксированных уровней квантования, а затем заменяется
на ближайшее из них. Величина напряжения (тока) исходного аналогового сигала может принимать теоретически бесконечное количество
произвольных значений (в пределах динамического диапазона сигнала), таким образом, уровень дискретного отсчета после квантования
неточно соответствует произвольному значению отсчета исходного аналогового сигнала. Эту погрешность принято называть шумами
квантования. Чем больше набор допустимых дискретных уровней квантования, тем меньше будут шумы квантования. На
практике, при обработке аудиосигналов часто применяется 256 уровней квантования и более.
После квантования следует процесс кодирования. При этом, в зависимости от дискретного уровня квантования, квантованный
отсчет заменяется двоичным числом, иначе называемом цифровым словом которое является кодом исходного аналогового сигнала
в фиксированный момент времени. Таким образом, цифровой сигнал представляет собой последовательность цифровых слов, записываемых
через равные интервалы в цифровую память.
Системы счисления и кодовые слова
Сегодня практически всем известно, что в современной цифровой и вычислительной технике используется двоичная система
счисления, оперирующая знаками (0, 1), а не в привычная десятичная (0—9) система, используемая человеком. Это
может показаться довольно ограниченным, потому что означает, что человек привык вести счет в каждом разряде считать до девяти,
в то время, как компьютер считает только до одного. Решением в обоих случаях является масштабирование системы счета. Каждый
раз при достижении 9 для добавления 1, мы записываем в число новый разряд, как масштабированную единицу, но это неудобный
термин, поэтому мы называем его «десять». Нет причин по которым было бы нельзя масштабировать десятки: «сотни, десятки, и
единицы», — как учат в начальной школе. Масштабирование показано более формально в табл. 4.1.
| Таблица 4.1 |
| тысячи | сотни | десятки | единицы | десятые | сотые | тысячные |
| 1000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1000 |
| 103 | 102 | 101 | 100 |
10-1 | 10-2 | 10-3 |
Термины «сотни, десятые», и т. п. являются просто степенью основания системы, в этом случае 10. Двоичная система
счисления строится точно так же, но так как в ней вместо основания «10» используется основание «2», ее масштабная таблица
выглядит иначе (см. табл. 4.2).
| Таблица 4.2 |
| 32 | 16 | 8 | 4 | 2 | 1 | 1/2 | 1/4 | 1/8 | 1/16 | 1/32 |
| 25 | 24 | 23 | 22 | 21 |
20 | 2-1 | 2-2 | 2-3 | 2-4 | 2-5 |
Таким образом, несмотря на то, что в двоичной системе используется только 0 и 1, с помощью комбинаций многоразрядных
чисел (кодовых слов), содержащих только эти символы, можно выразить любое десятичное число. В цифровой и вычислительной
технике, каждый разряд кодового слова принято называть битом информации. Таким, образом, если двоичное число (кодовое
слово) состоит из четырех разрядов, то говорят, что оно содержит четыре бита информации, или является четырехбитным.
При аналого-цифровом преобразовании, разрядность цифрового кода (то есть число бит в кодовых словах) напрямую зависит
от числа уровней квантования. Чаще всего, разрядность кодовых слов берется кратным восьми. Используются 8-битовые, 16-битовые,
24-битовые, 32-битовые и т. п. кодовые слова. В цифровой и вычислительной технике 8 бит информации называют одним байтом.
Поскольку, для каждого бита информации возможно два состояния — 1 и 0, нетрудно подсчитать, какое количество дискретных
квантованных уровней сигнала может быть описано однобайтным, двухбайтным и т. п. Итак, общее число различных уровней, которые
могут быть описаны 8-разрядным (восьмибитным или однобайтным) кодовым словом, равно 28 = 256, а 16-разрядным словом,
— 216 = 65536. Подобным образом, 24-битная система допускает 224 = 16 777216 различных уровней, но
требуется в полтора раза больше памяти для сохранения каждого слова (24/16 = 1S), чем в 16-битной.
Как правило (игнорируя вспомогательные добавочные псевдослучайные сигналы, необходимые, как для повышения помехозащищенности,
так и для других целей), динамический диапазон (ДД) цифровой системы определяется следующим образом:
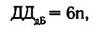
где п = количество бит.
Таким образом, теоретический динамический диапазон 16-разрядной системы равен 6 х 16 = 96 дБ.
Говоря о цифровой технике, всегда важно помнить, что с увеличением числа уровней квантования, а также с повышением частоты
дискретизации, точность цифровогопредставления сигнала возрастает, но при этом требуются существенно большие ресурсы цифровой системы (быстродействие,
память), поскольку неизбежно растет разрядность кодовых слов.
Быстрое преобразование Фурье (БПФ)
Уже неоднократно обсуждалось, что любой процесс можно представить двояко — во временной или в частотной области. На экране
осциллографа мы видим графическую зависимость уровня исследуемого процесса от времени — это есть временное представление.
На экране анализатора спектра, мы видим зависимость уровня того же процесса от частоты — это есть частотное представление.
При оценке нелинейных искажений очень полезно иметь спектр исследуемого сигнала, однако, как уже говорилось выше, анализатор
спектра прибор дорогой и сложный. Однако, при помощи звуковой карты и несложного программного обеспечения, в анализатор спектра
(конечно, далеко не самый хороший, но вполне приемлемый) нетрудно превратить обычный персональный компьютер. Основное преимущество
цифрового представления сигналов, — это возможность применения для их обработки сложных математических алгоритмов. Аналитическая
взаимосвязь между временным и частотным представлением процессов была установлена выдающимся математиком Фурье, и такое преобразование
носит его имя.
Вычислительный алгоритм, лежащий в основе работы программных средств по обработке оцифрованных звуковых сигналов, осуществляющий
их преобразование из временной формы представления в частотную, носит название быстрого преобразования Фурье (БПФ).
Алгоритм БПФ, не смотря на его крайне широкое применение, тоже имеет свои особенности и ограничения. В частности, вся
математика БПФ построена на предположении, что обрабатываемый сигнал является периодически повторяющимся процессом. Это
предположение может показаться тривиальным, но оно имеет важные последствия.
Любые реальные сигналы всегда случайны и далеко не всегда периодичны. В реальном сигнале очень трудно выделить один период
с достаточной точностью, что вызовет существенную погрешность при обработки с помощью БПФ. Для уменьшения этой ошибки, обработку
производят не по одному периоду, а по значительно большему их количеству. При этом точность обработки существенно повышается,
но она требует серьезных аппаратных ресурсов, поскольку требуется одновременная запись в память большого количества кодовых
слов, пропорционального количеству одновременно обрабатываемых периодов.
Другим способом уменьшения количества шагов является кадрирование — искусственное выделение периодичности, применяя
так называемые окна к записям форм сигналов. В этом контексте, окно является переменным весовым коэффициентом.
При этом значения выборок в концах записей форм сигналов умножаются на нуль, а к промежуточным значениям в середине выборок
применяется больший весовой коэффициент (≤1). Поскольку любое число умноженное на нуль равно нулю, это
делает концы выборок нулевыми, — это позволяет записи формы сигнала повторять без сбоев (рис. 4.4.)
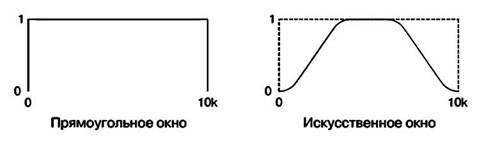
Рис. 4.4 Кадрирование, вызывающее периодичность
Так как кадрирование вносит определенные искажения в запись формы сигнала, его применение будет также искажать и результаты
БПФ. В процессе кадрирования либо происходит «сброс» энергии элементов дискретизации с высокими амплитудами в смежные элементы
дискретизации, что порождает видимую «кайму» в окрестностях дискретных спектральных составляющих, имеющих высокие амплитуды
на экране анализатора, или изменяются амплитуды отдельных составляющих. Так как процесс дискретизация преобразует непрерывное
время в дискретные отсчеты, то и результатом БПФ должны быть дискретные частотные (спектральные) составляющие, называемых
элементами дискретизации. Следовательно, все «кадры» и «окна» всего лишь позволяют находить компромисс между разрешающей
способностью по частоте и амплитуде.
Кадр, в котором выборка практически не претерпевает изменений (поскольку запись формы сигнала всего кадра умножается
на постоянное значение — 1), называется прямоугольным кадром. Так как прямоугольный кадр практически не изменяет значения
выборок, он не вызывает разброс между элементами дискретизации и предлагает лучшую разрешающую способность по частоте. К
сожалению, амплитуды отдельных составляющих могут быть интерпретированы с ошибками, потому что при кадрировании искусственно
изменяется периодичность. И наоборот, так называемый кадр Блэкмана-Харриса (Blackman—Harris) изменяет концы записи формы
сигнала, чтобы предотвратить нарушение периодичности, что вызывает разброс между элементами дискретизации, но улучшает разрешающую
способность по амплитуде.
Наилучшие результаты измерения искажений с использованием алгоритма БПФ получаются при синхронизации генератора с системой
БПФ, для того чтобы могли записываться только полные циклы без фазовых ошибок, позволяя использовать прямоугольный кадр.
Если истинное синхронное БПФ не возможно, то полезный компромисс — это настройка анализатор на основной частоте и
подгонка частоты измерительного генератора для получения минимальной «каймы» в окрестностях составляющей с самой высокой
амплитудой.
Если записи формы сигнала зафиксированы многократно, то можно их усреднить, чтобы уменьшить ошибки. Это очень мощная
методика, несмотря на то, что она замедляет скорость измерений.
|



