|
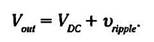
Переменное напряжение пульсаций равномерно колеблется относительно линии VDC и при положительной полуволне
достигает амплитудного значения Vpeak, следовательно,
Накопительный конденсатор заряжается до амплитудного значения выходного напряжения выпрямителя, напряжение пульсаций
вычитается из него и, таким образом, снижает выходное напряжение. Выходное напряжение Vout можно
представить как бы состоящим из двух составляющих: составляющей напряжения постоянного тока, представленной как бы в идеальном
виде, VDC, и наложенной на него переменной составляющей напряжения остаточных пульсаций, υripple.
Удобство такого подхода проявляется в том, что последующий фильтр отсекает переменную составляющую тока пульсаций, оставляя
только чисто постоянную составляющую.
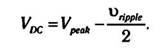
Если обратиться к ранее рассмотренному примеру, для которого υripple = 18 В, а амплитудное
значение напряжения Vpeak = 325 В, то напряжение постоянного тока, которое будет получено после
идеальной последующей фильтрации переменной составляющей, составит:
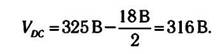
В заключение следует отметить, что во всех случаях величина постоянного напряжения всегда будет уменьшаться на половину
значения напряжения пульсаций.
Пульсирующая составляющая постоянного тока и угол проводимости
После рассмотрения проблем с напряжением остаточных пульсаций необходимо рассмотреть ток пульсирующей составляющей. Последний
фактически составляет ток, необходимый для полного восстановления заряда на конденсаторе во время каждого полупериода. Чтобы
определить величину этого тока, необходимо найти значение угла проводимости, который представляет время, в течение которого
диоды остаются во включенном состоянии и одновременно заряжается конденсатор (рис. 6.8).
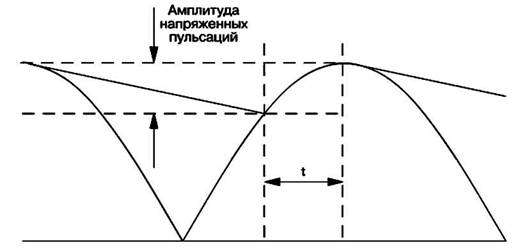
Рис. 6.8 Определение угла проводимости по величине напряжения пульсаций
Для определения этой величины надо начать отсчет с момента времени, когда конденсатор полностью заряжен. Так как известно
значения напряжения пульсаций, то можно определить абсолютное значение напряжения на конденсаторе в тот момент времени, когда
диод проводит ток. Тогда напряжение на выходе выпрямителя (если для простоты изложения пренебречь полярностью напряжения)
составляет:
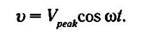
В тот момент времени, когда диод начинает проводить ток, напряжение на конденсаторе должно составлять:
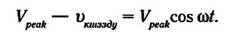
После преобразования уравнения получим следующие выражения:

Если в это уравнение подставить значения, взятые из ранее рассмотренного примера (рис. 6.6) и учесть, что значения углов
выражаются в радианной мере, а не в градусной, то время t будет равно:
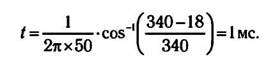
Таким образом, ток, потребляемый конденсатором от силового трансформатора, протекает только 1 мс в течение каждых 10
мс, равных длительности полупериода, что составит всего 10% от общего времени. Поэтому следует ожидать, что ток пульсаций
будет представлять очень острые и высокие импульсы косинусоидальной формы (рис. 6.9).
Также можно определить величину тока, если воспользоваться следующим соотношением:
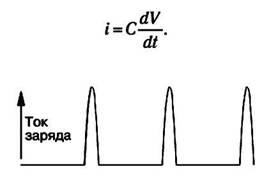
Рис. 6.9 Форма импульсов тока пульсаций
После его дифференцирования получим:
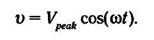
а, подставив полученное выражение в формулу для тока, получим в окончательном виде:
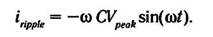
Если в это выражение подставить ряд значений, использовавшихся в ранее приведенном примере, то для тока пульсаций получим:
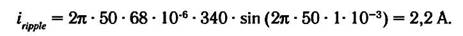
Однако для этого необходимо прежде получить выражение, отражающее скорость изменения напряжения во времени, поэтому необходимо
использовать исходное выражение
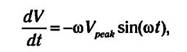
Таким образом, полученное значение тока пульсаций значительно превышает ток, протекающий в нагрузке и равный 120 мА!
Можно также попытаться сделать приближенную оценку. Заряд равняется произведению величины тока на время, что эквивалентно
площади, очерченной кривой тока по оси времени. Если конденсатор должен заряжаться в течение одной десятой времени, необходимого
для его разряда, то можно допустить, что для этого понадобится десятикратное значение тока (так как Q = It). Это
определяет значение тока, равное 1,2 А. Однако, ранее было установлено, что форма импульсного тока заряда отличается от прямоугольной
формы, поэтому, площадь, занимаемая таким импульсом будет меньше, чем площадь прямоугольника с эквивалентными значениями
высоты и ширины, что и объясняет полученную разницу в оценках.
В заключение можно заметить, что полученный результат хотя и является неожиданно большим, однако он вовсе не является
нереальным.
Рассмотренная модель предсказывает максимально возможное значение тока пульсаций, поэтому стоит проверить, что выпрямитель
и конденсатор смогут выдержать такие импульсы токов, а это можно сделать, сравнивая величины амплитудных значений токов.
На практике амплитудное значение тока пульсаций снижается за счет следующих факторов:
• последовательно включенного сопротивления, которое образуется за счет: прямого сопротивления диода, последовательного
эквивалентного сопротивления конденсатора, сопротивления подводящих проводов, сопротивления обмоток трансформатора (вторичной
с учетом эквивалентного приведенного сопротивления первичной обмотки);
• насыщения сердечника трансформатора.
В результате действия этих факторов амплитудное значение тока пульсаций находится, как правило, в диапазоне от четырех-
до шестикратного значения постоянного тока нагрузки. Можно рассмотреть следующий пример, взятый из практики. В трансформаторе,
работающем на выпрямитель, который был собран из кремниевых диодов, включенных по мостовой схеме, имел на выходе емкостной
фильтр и обеспечивал постоянное напряжение 108 В с постоянным током нагрузки 35 мА, величина амплитудного значения тока
пульсаций составляла Iripple(pk)= 160 мА, то есть отношение токов составляло 4,6:1.
Ламповые диоды обладают значительно более высоким собственным сопротивлением по сравнению с кремниевыми, а в ряде случаев
требуют использования дополнительного последовательно включенного сопротивления в связи с ограниченными возможностям по
отношению к большим значениям токов пульсаций, поэтому величина отношения токов пульсации к величине выпрямленного постоянного
тока Iripple / IDC скорее всего будет еще меньше. Для исследования высоковольтного
источника питания с напряжением 300 В, в котором применялись выпрямительная лампа GZ34, и полипропиленовый накопительный
конденсатор с емкостью 47 мкФ, использовался измеритель тока Tektronix TCP202 с рабочей частотой 50 МГц (рис. 6.10).
Импульсы тока пульсаций содержат гармоники частоты пульсаций 100 Гц, которые теоретически попадают не только в полосу
звуковых частот, причем не только в область низких частот, но и в нижнюю часть области высоких звуковых частот. Пример спектрограммы
токов пульсаций, протекающих в накопительном конденсаторе приведен на рис. 6.11. Эта спектрограмма была получена на осциллографе,
в котором предусмотрен режим быстрого преобразования Фурье (FFT). Полученный спектр занимает диапазон от постоянного тока
(левая граница) до частоты 1,25 кГц (правая граница). На спектрограмме явно видна первая (основная) гармоника на частоте
100 Гц, а также высшие гармоники на кратных первой частотах. Хотя линейный вертикальный масштаб использованного быстрого
Фурье-преобразования предполагал, что гармоники затухают достаточно быстро, просмотр спектрограммы в логарифмическом масштабе
позволяет обнаружить, что уровень гармоник с частотой 2,5 кГц всего лишь на 45 дБ ниже уровня основной гармоники с частотой
100 Гц.
|